
|
|
11. КОЛИЧЕСТВЕННЫЕ МЕТОДЫ АНАЛИЗА И ИХ ИСПОЛЬЗОВАНИЕ ДЛЯ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
Количественные, т.е. экономико-математические, методы существенно обогатили арсенал приемов экономического анализа хозяйственной деятельности. Их широкое применение обусловлено успехами прикладной математики и кибернетики и быстрым освоением новых форм хозяйствования, демократизацией управления народным хозяйством. Дальнейшее совершенствование производства, переход на интенсивные методы хозяйствования значительно усложняют хозяйственные связи и технико-экономические процессы, что ведет к возникновению новых проблем в экономическом анализе. Эти проблемы следует решать оперативно и точно. В таких условиях старые, традиционные методы и технические средства часто оказываются недостаточно эффективными, поэтому необходимы математические методы и ЭВМ.
Применение математических методов и ЭВМ в анализе хозяйственной деятельности требует:
• системного подхода к изучению экономики первичного звена народного хозяйства, учета всего множества существенных взаимосвязей между различными сторонами его деятельности;
• разработки научных классификаций задач экономического анализа и экономико-математических методов их решения;
• совершенствования системы экономической информации о работе предприятия;
• создания вычислительной сети и автоматизированных рабочих мест экономистов, оснащенных современными персональными ЭВМ и осуществляющих хранение, обработку и передачу аналитической информации для принятия управленческих решений;
• организации непрерывного обучения аналитиков и экономистов-производственников новым методам и приемам экономико-математического моделирования хозяйственной деятельности, обработки данных и программирования на ЭВМ.
Проникновение математики и ЭВМ в экономический анализ - объективный процесс. Происходит обогащение экономического анализа, развивается теория комплексного экономического анализа, имитационное моделирование для анализа конкретных хозяйственных ситуаций, перспективный экономический анализ, разрабатываются интегральный и обобщенный интегральный методы анализа факторных влияний на показатели хозяйственной деятельности, методы комплексной оценки хозяйственной деятельности.
11.1. Общая характеристика и классификация количественных методов анализа
Систематизировать применяемые в анализе хозяйственной деятельности математические методы можно по различным признакам. Наиболее целесообразной и простой представляется классификация экономико-математических методов по трем признакам: 1) по содержанию метода, т.е. принадлежности к определенному разделу современной математики; 2) по содержанию задачи экономического анализа; 3) по содержанию аналитической деятельности, т.е. принадлежности к определенному виду экономического анализа. Ниже в таблице приведена примерная классификация экономико-математических методов в соответствии с наиболее часто применяемыми разделами современной математики.
Сформулированная математическая задача экономического анализа может быть решена одним из наиболее разработанных математических методов, поэтому приведенная классификация в значительной мере условна. Например, задачи управления запасами могут решаться методами математического программирования и с применением теории массового обслуживания. При сетевом планировании и управлении можно использовать самые различные методы. Понятие «исследование операций» иногда определяется настолько широко, что охватывает все экономико-математические методы.
Примерная классификация экономико-математических методов в анализе хозяйственной деятельности
  Методы элементарной математики используются в обычных традиционных экономических расчетах при обосновании потребностей в ресурсах, учете затрат на производство, обосновании планов, проектов, балансовых расчетах и т.д.
Выделение методов классического математического анализа на схеме обусловлено тем, что они применяются не только в рамках других методов, например методов математической статистики и математического программирования, но и отдельно. Так, факторный анализ изменения многих экономических показателей может быть осуществлен при помощи дифференцирования и интегрирования.
Широкое распространение в экономическом анализе имеют методы математической статистики и теории вероятностей. Эти методы применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс. Статистические методы как основное средство изучения массовых, повторяющихся явлений играют важную роль в прогнозировании поведения экономических показателей. Когда связь между анализируемыми характеристиками не детерминированная, а стохастическая, то статистические и вероятностные методы есть практически единственный инструмент исследования. Наибольшее распространение из математико-статистических методов в экономическом анализе получили методы множественного и парного корреляционного анализа.
Для изучения одномерных статистических совокупностей используются вариационный ряд, законы распределения, выборочный метод. Для изучения многомерных статистических совокупностей применяют корреляции, регрессии, дисперсионный и факторный анализ.
Эконометрические методы строятся на синтезе трех областей знаний: экономики, математики и статистики. Основа эконометрии - экономическая модель, под которой понимается схематическое представление экономического явления или процесса при помощи научной абстракции, отражения их характерных черт. Наибольшее распространение получил метод анализа «затраты - выпуск». Это матричные (балансовые) модели, строящиеся по шахматной схеме и позволяющие в наиболее компактной форме представить взаимосвязь затрат и результатов производства. Удобство расчетов и четкость экономической интерпретации - главные особенности матричных моделей. Это важно при создании систем механизированной обработки данных, при планировании производства продукции с использованием ЭВМ.
Математическое программирование - важный раздел современной прикладной математики. Методы математического (прежде всего линейного) программирования служат основным средством решения задач оптимизации производственно-хозяйственной деятельности. По своей сути эти методы есть средство плановых расчетов. Их ценность для экономического анализа выполнения планов состоит в том, что они позволяют оценивать напряженность плановых заданий, определять лимитирующие группы оборудования, виды сырья и материалов, получать оценки дефицитности произведенных ресурсов и т.п.
Под исследованием операций имеются в виду разработка методов целенаправленных действий (операций), количественная оценка полученных решений и выбор наилучшего из них. Предметом исследования операций являются экономические системы, в том числе производственно-хозяйственная деятельность предприятий. Цель - такое сочетание структурных взаимосвязанных элементов систем, которое в наибольшей степени отвечает задаче получения наилучшего экономического показателя из ряда возможных.
Экономическая кибернетика позволяет анализировать экономические явления и процессы в качестве очень сложных систем с точки зрения законов и механизмов управления и движения информации в них. Наибольшее распространение в экономическом анализе получили методы кибернетического моделирования и системного анализа.
Эвристические методы (решения) - это неформализированные методы решения экономических задач, связанных со сложившейся хозяйственной ситуацией, на основе интуиции, опыта, экспертных оценок специалистов и т.д.
11.2. Детерминированное моделирование факторных систем хозяйственной деятельности
Наиболее важными в анализе хозяйственной деятельности являются модели исследования взаимосвязей между экономическими показателями. Так, между показателями объема продукции (ТП), численности работающих (Ч) и производительности труда одного работающего (В) существует функциональная связь:
ТП = Ч-В. (1)
Если данные показатели работы предприятия исследуются за годовой период деятельности, то возможна более детализированная формула связи:
ТП=У-Д-Т-ВЧ. (2)
Эта формула устанавливает зависимость объема продукции от изменений удельного веса числа рабочих в общей численности работающих (У), среднего количества дней, отработанных одним рабочим за год (Д), средней продолжительности рабочего дня (Т), средней часовой производительности труда одного рабочего (ВЧ). Выявление и исследование подобных зависимостей между экономическими показателями осуществляются при помощи методов детерминированного моделирования. Зависимости вида (1) и (2) представляют собой факторные модели показателя объема продукции, удовлетворяющие различной степени детализации анализа этого показателя.
Процесс построения факторной модели для анализируемого экономического показателя хозяйственной деятельности может быть осуществлен как формальным, так и эвристическим путем, на основе качественного анализа сущности экономического явления, отражаемого через данный результативный показатель. Факторное моделирование основывается на экономических критериях выделения факторов как элементов факторной системы: причинности, достаточной специфичности, самостоятельности существования, учетной принадлежности. С формальной точки зрения факторы, включаемые в факторную модель, должны быть количественно измеримыми.
В детерминированном моделировании можно выделить небольшое число типов конечных факторных моделей, наиболее часто встречающихся в анализе хозяйственной деятельности.
1. Аддитивные модели:
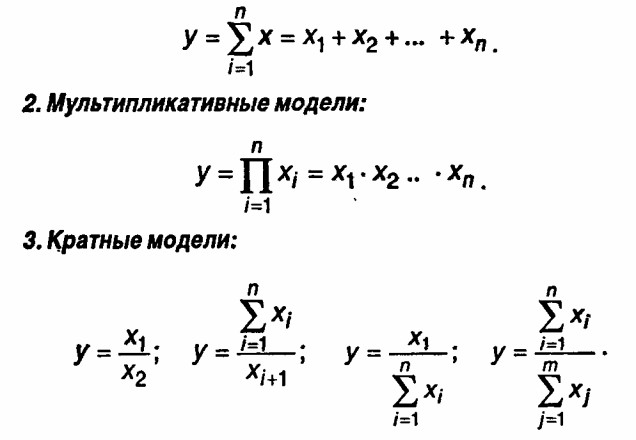 4. Смешанные модели - любая комбинация первых трех типов, где у - результативный показатель (исходная факторная модель); хi - факторы (факторные показатели).
Применительно к классу детерминированных факторных моделей различают следующие основные приемы моделирования.
 Метод расширения факторной системы: исходная факторная система - у = a1/a2. Если и числитель, и знаменатель дроби «расширить» умножением на одно и то же число, то получим новую факторную систему:
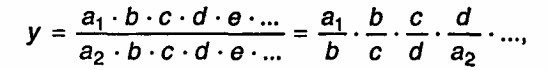 т.е. мультипликативную модель вида у = Пхi .
Метод сокращения факторной системы: исходная факторная система у = a1/a2 . Если и числитель, и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему (при этом, естественно, должны быть соблюдены правила выделения факторов):
В данном случае имеем конечную факторную систему вида
Итак, сложный процесс формирования уровня изучаемого показателя может быть разложен различными приемами по его составляющим (факторам) и представлен в виде модели детерминированной факторной системы. При использовании детерминированных моделей необходимо обратить внимание на следующее.
1. Детерминированная модель исследуемого явления включает определенные элементы этого явления. Закономерности прямо перенесенных элементов в данной модели остаются нераскрытыми. Например, производительность труда, вычисляемая через объем выпускаемой продукции, переносит в модели объема выпускаемой продукции в нераскрытом виде определенные закономерности формирования последнего (влияние фактора цен, структуры и т.п.).
2. Границей составления детерминированных моделей является длина непрерывной цепи прямых связей.
3. При детерминированном подходе модель полностью определяется уровнем профессионального качественного анализа.
4. В большинстве случаев при детерминированном подходе не учитывается влияние одновременно действующих факторов. Например, элиминирование факторных влияний при анализе отклонений объема производства продукции по факторам использования средств труда, предметов труда и живого труда приводит к повторному отражению одних и тех же закономерностей формирования объема производства продукции.
5. В детерминированной модели, отражающей теоретически предполагаемые прямые связи, не учитывается взаимозаменяемость факторов.
Перечисленные недостатки детерминированного подхода преодолеваются при стохастическом моделировании хозяйственной деятельности.
11.3. Методы количественной оценки влияния факторов на результативный показатель
Если известна факторная модель обобщающего экономического показателя, то следующим этапом анализа является определение величины абсолютного или относительного изменения этого показателя за счет изменений факторных показателей. Разработано множество методов определения такого влияния: метод разниц, метод цепных подстановок, индексный метод, метод логарифмирования, метод долевого участия, ряд других методов. За исключением метода логарифмирования все методы базируются на установлении приоритетности факторов. Это существенный недостаток данных методов. Поэтому все большее распространение в теории и практике экономического анализа находит интегральный метод оценки факторных влияний.
ЦЕПНЫЕ ПОДСТАНОВКИ. Данный метод - это последовательная замена базисного значения фактора на фактическое для определения факторных влияний на результативный показатель хозяйственной деятельности. При помощи метода цепных подстановок последовательно выделяют влияние на результативный показатель только одного фактора и исключают влияние остальных. Метод дает удовлетворительные оценки факторных влияний при строгом соблюдении последовательности подстановок, четком разграничении количественных (экстенсивных) и интенсивных факторов. Суть метода заключается в следующем. Пусть задана функциональная связь обобщающего (результативного) показателя с n факторами: в общем виде у = f (a, b, c, d,...,); мультипликативная форма связи: у = ab; кратная форма связи у = а/b. Если известны базисное и фактическое значения показателей, то общее абсолютное отклонение показателей за период составит: в общем виде: ?y =f (a1, b1, c1, d1,...)-f (a0, b0, c0, d0, ...); для мультипликативной формы связи: ?у = a1b1 - а0b0; для кратной модели: ?y = a1b1 - a0b0.
Используя цепные подстановки, определяем расчетные значения обобщающего показателя путем последовательной замены базисного значения первого, второго и т.д. факторов на их фактические значения. Разность между двумя расчетными значениями показателя в цепи подстановок определит влияние того фактора, для которого произведена замена базисного значения на фактическое. В общем виде
?y =f (а1, b0,c0,d0,...) - f (а0,b0,c0,d0,…) - влияние фактора а;
ЛУь = f(ai,bi,Co,do, ...)-Ца-1,Ьо,Со,с1о,...) -влияние фактора b;
......... и т.д.
Для кратной формы связи, при тех же предположениях, что и для мультипликативной модели:
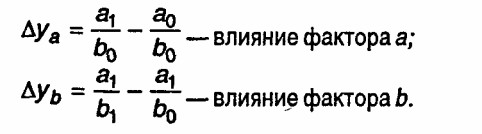 Заметим, что при тех же предположениях другая последовательность подстановок факторов даст неверные оценки факторных влияний.
ИНДЕКСНЫЙ МЕТОД.
Индексы - относительные величины, характеризующие соотношение явлений во времени, пространстве и по сравнению с планом. Различают индексы индивидуальные, общие, агрегатные, факторные, переменного и фиксированного состава. Индексы применяют для характеристики динамики сложных совокупностей и измерения роли отдельных факторов в динамике обобщающих показателей хозяйственной деятельности. Метод построения общих индексов, позволяющих соотносить показатели по сложным совокупностям, составляет особый прием анализа, именуемый индексным методом.
Изучая зависимость объема выпуска продукции (N) на предприятии от изменений численности работающих (R) и производительности их труда (D), используют следующие индексы:
 Взаимосвязь показателей представляется индексной системой IN =IR•1D, которая позволяет вычислить общий абсолютный прирост объема продукции (?N) и прирост, вызванный изменениями факторов численности (?NR) и производительности труда работающих (?ND):
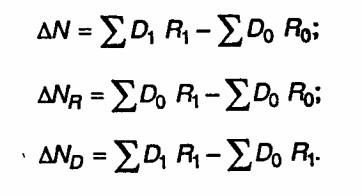 МЕТОД ДИФФЕРЕНЦИРОВАННОГО ИСЧИСЛЕНИЯ основан на формуле полного дифференциала. Для функции от двух переменных z = f (х, у) имеем полное приращение функции ?z:
 Таким образом, влияние фактора х на обобщающий показатель определяется по формуле
влияние фактора у:
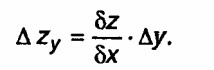 Логарифмический метод. Этот метод дает логарифмически пропорциональное распределение прироста показателя по анализируемым факторам. Для факторной системы z = ху абсолютное изменение показателя z за счет факторов х и у определяется по формулам:
 Интегральный метод дает наиболее общий подход к решению задач факторного анализа по разложению общего прироста показателя по факторным приращениям. В основе интегрального метода лежит интеграл Эйлера-Лагранжа, устанавливающий связь между приращением функции и приращением факторных признаков. Для функции z = f (х, у) имеем следующие формулы расчета факторных влияний.
1. По методу дифференцирования:
?zX = f'X • ?х - влияние фактора х,
где f'X - частная производная функции пох;
?zY = f'Y • ?у - влияние фактора у,
где f'Y - частная производная функции по у.
2. По интегральному методу:
?zX = ?f'X • dx - влияние фактора х;
?zY = ?f'Y • dy - влияние фактора у.
ИНТЕГРАЛЬНЫЙ МЕТОД. Данный метод является обобщением метода цепных подстановок и логарифмического метода. При некоторых предположениях они выводятся из интегрального метода как частные случаи.
Для применения интегрального метода требуются знание основ дифференциального исчисления, техники интегрирования и умение находить производные различных функций. Вместе с тем в теории анализа хозяйственной деятельности для практических приложений разработаны конечные рабочие формулы интегрального метода для наиболее распространенных видов факторных зависимостей, что делает этот метод доступным для каждого аналитика. Приведем некоторые из них.
1. Факторная модель типа и = ху:
?u = ?uX + ?uY;
?uX = yO ?х + (?x ·?y)/2;
?uY = xO?y + (?x · ?y)/2;
?uY = ?u - ?uX.
2. Факторная модель типа u = xyz:
?u = ?uX + ?uY + ?uY;
?uX = yO • zO • ?x + 1/2 yO • ?x • ?z + 1/2zO • ?x • ?y + 1/3?y • ?z • ?x;
?uY = xO • zO • ?y + 1/2xO • ?y • ?z + 1/2 zO • ?х • ?y + 1/3?y • ?z • ?х;
?uZ = xO • yO • ?z + 1/2xO • ?z • ?y + 1/2yO • ?z • ?x + ?y • ?z • ?x.
3. Факторная модель типа и = x/y:
?u = ?uX + ?uY;
?uX = ?x/?y • ln ? y1/y0?;
?uY =?u - ?uX.
 Интегральный метод дает точные оценки факторных влияний. Результаты расчетов не зависят от последовательности подстановок и последовательности расчета факторных влияний. Метод применим для всех видов непрерывно дифференцируемых функций; не требует предварительных знаний о том, какие факторы количественные, какие качественные. Вместе с тем данный метод не работает при наличии взаимосвязей между факторами, исследовании влияний не только от исходных факторов, но и функций от них.
11.4. Стохастическое моделирование факторных систем хозяйственной деятельности
Исследование взаимных распределений значений экономических показателей и нахождение соотношений функционирования производственных систем представляет следующий важный класс задач анализа хозяйственной деятельности, например, задачу определения средней линии изменений объема продукции (ТП) в зависимости от изменения численности работающих (Ч) и производительности труда (В) по заданной совокупности предприятий. Такая задача решается методами стохастического моделирования. Здесь моделируется конкретное аналитическое выражение для зависимости
ТП= f (Ч,В).
Стохастическое моделирование все шире применяется в перспективном и сравнительном экономическом анализе, комплексной оценке результатов хозяйственной деятельности, анализе напряженности плановых заданий. Наряду с хорошо зарекомендовавшими себя методами корреляционного и регрессионного анализа, производственных функций получает широкое распространение моделирование факторных систем хозяйственной деятельности на основе методов современного факторного анализа, имитационного моделирования, матричных моделей.
Можно выделить следующие наиболее типичные классы задач анализа хозяйственной деятельности, для решения которых применяются методы стохастического моделирования:
• изучение наличия, направления и интенсивности связей показателей хозяйственной деятельности;
• ранжирование и классификация факторов экономических явлений;
• выявление аналитической формы связи между показателями;
• ранжирование и классификация объектов хозяйствования;
• выявление наиболее информативных (обобщающих) показателей хозяйственной деятельности;
• анализ структурных сдвигов в совокупности объектов анализа;
• нахождение общих закономерностей функционирования объекта;
• построение усредненных нормативов хозяйственной деятельности.
Для решения перечисленных задач применяются такие математико-статистические методы стохастического моделирования, как группировка многомерных наблюдений, корреляционный и регрессионный анализ, таксономический метод, дисперсионный анализ, методы причинного анализа, компонентный анализ.
В основе стохастического моделирования лежит возможность построения соотношений функционирования объекта анализа на основе статистического обобщения закономерностей изменения значений показателей хозяйственной деятельности. Например, на основе анализа зависимости фондоотдачи от показателей организационно-технического уровня по совокупности объектов литейного производства построена модель стохастической зависимости вида
f = а1 х1 + а2 x2 + а3 x3 + а4 x4 + а5 x5 + а6 x6 > где х1, x2, ..., x6 - показатели организационно-технического уровня;
а1, а2,....а6 - коэффициенты регрессии, характеризующие интенсивность влияния показателей организационно-технического уровня на фондоотдачу.
Эта зависимость выполняется в среднем для всей совокупности.
Необходимые предпосылки стохастического моделирования: возможность составления совокупности наблюдений (измерений); качественная однородность совокупности относительно изучаемых связей; достаточная размерность совокупности; наличие соответствующих методов.
Прямой стохастический факторный анализ имеет свои особенности. Если в случае прямого детерминированного факторного анализа исходные данные представлены конкретными числами, то в случае прямого стохастического факторного анализа они заданы выборкой (временной или пространственной). Решение задач стохастического факторного анализа более трудоемко, так как требует:
• глубокого экономического исследования для выявления основных факторов, влияющих на результативный показатель;
• подбора вида стохастической зависимости, который бы наилучшим образом отражал действительную связь изучаемого показателя с набором факторов;
• разработки метода, позволяющего определить влияние каждого фактора на результативный показатель.
Если результаты прямого детерминированного анализа должны получиться точными и однозначными, то стохастического - с некоторой вероятностью (надежностью), которую следует оценить.
Примером прямого стохастического факторного анализа является регрессионный анализ производительности труда и других экономических показателей.
11.5. Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ - классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки). В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессионного анализа.
Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случав между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.).
ОСНОВНЫЕ МОДЕЛИ КОРРЕЛЯЦИОННОГО АНАЛИЗА. Такими моделями являются: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации.
Линейный коэффициент парной корреляции (р) определяется по формуле:
где х, у - значения факторного и результативного показателей соответственно;
х, у - средние значения соответствующих показателей;
?X, ?Y - средние квадратические отклонения (стандартные отклонения показателей х и у);
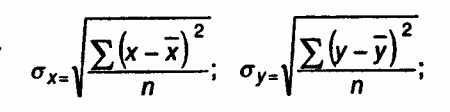 n - количество наблюдений в совокупности.
Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак «+» означает наличие прямой связи между показателями. Знак «-» - наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы.
Часто в анализе хозяйственной деятельности при изучении связи между показателями х и у требуется исключить воздействие третьего показателя z, выступающего как общий фактор изменения анализируемых показателей. Для этого используется коэффициент частной корреляции (rx,y,z), свойства которого совпадают со свойствами коэффициента парной корреляции:
где rxy, rxz, ryz - коэффициенты парной корреляции между соответствующими показателями.
Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:
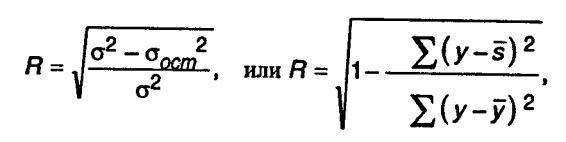 где ?2 - общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;
?ост2 - остаточная дисперсия в ряду у, отражающая влияния всех факторов, кроме х;
у - среднее значение результативного показателя, вычисленное по исходным наблюдениям;
s - среднее значение результативного показателя, вычисленное по уравнению регрессии.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами. При значении 0,3 < R < 0,6 говорят о средней тесноте связи. При R > 0,6 говорят о наличии существенной связи.
Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R2. Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия (?2) равна сумме межгрупповой дисперсии (?2) и средней из групповых дисперсий ?i2):
?2 = ?2 + ?i2.
Межгрупповая дисперсия характеризует колеблемость результативного показателя за счет изучаемого фактора, а средняя из групповых дисперсий отражает колеблемость результативного показателя за счет всех прочих факторов, кроме изучаемого.
Математические модели корреляционного анализа в форме коэффициентов имеют ограниченные аналитические возможности. Зная лишь направление ковариации показателей и тесноту связи, невозможно определить закономерности формирования уровня результативного показателя под влиянием исследуемых факторов, оценить интенсивность их влияния, классифицировать факторы на основные и второстепенные. Для этих целей используются модели регрессионного анализа. Линейная модель (уравнение) регрессионного анализа может быть представлена в виде
у = bo + b1x1 + b2x2 +... + bnxn,
где у - результативный показатель;
x1, x2, ..., xn - факторные модели;
b0, b1, b2, ..., bn - коэффициенты регрессии.
Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то b0 равняется среднему значению результативного показателя в совокупности. Коэффициенты b1, b2, ..., bn показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений).
Аналитические достоинства регрессионных моделей заключаются в том, что, во-первых, точно определяется фактор, по которому выявляются резервы повышения результативности хозяйственной деятельности; во-вторых, выявляются объекты с более высоким уровнем эффективности; в-третьих, возникает возможность количественно измерить экономический эффект от внедрения передового опыта, проведения организационно-технических мероприятий.
Рассмотрим теперь задачу 1 из заданий по анализу регрессии, приведенную на с. 300-301. Построим линейную регрессионную модель по методу наименьших квадратов. Обозначим через ti, год выпуска автомобилей, а через Ni - объем выпуска в этом году. Данные, представленные в таблице, изобразим на графике, представленном ниже.
В качестве функции линейной регрессии возьмем
Ni = а + bti, i = 1,2,...,32.
Критерий метода наименьших квадратов в этом случае имеет вид
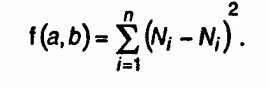 Выпуск автомобилей по годам (N - тыс. шт.)
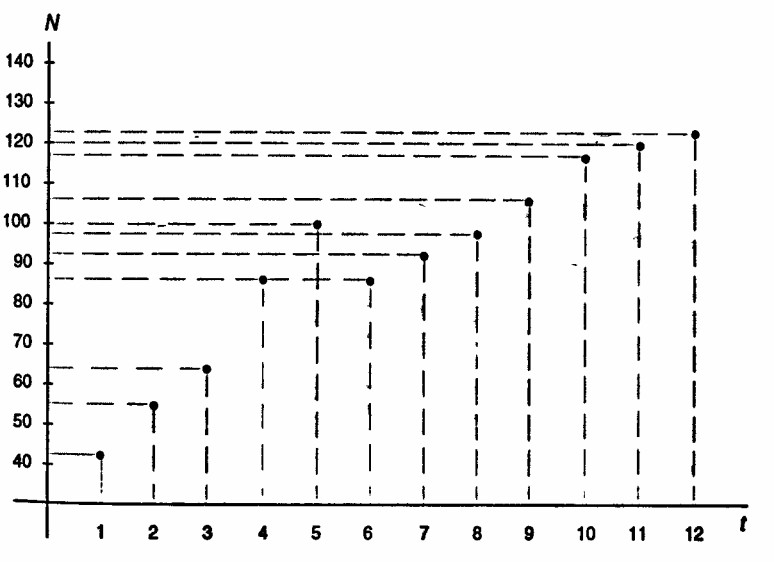    Один из математических результатов теории линейной регрессии говорит, что оценка N, является несмещенной оценкой с минимальной дисперсией в классе всех линейных несмещенных оценок.
Остаточная дисперсия вычисляется по формуле
Современный факторный анализ - направление многомерного статистического анализа, которое позволяет выявить внутренние, непосредственно неизмеримые переменные (факторы) между коррелирующими показателями хозяйственной деятельности. Различают два основных метода современного факторного анализа: метод главных компонент и классический факторный анализ.
Модель метода главных компонент выглядит так:
zj = aj1F1 + aj2F2 +...+ ajnFn,
где zj - исходные показатели;
F1, F2, ..., Fn - компоненты (факторы);
ajn - факторные нагрузки на j-ю переменную.
Модель классического факторного анализа выглядит несколько иначе:
zj = aj1F1 + aj2F2 +...+ ajmFm + ajFj + uj,
где исходная переменная zj линейно зависит от m общих факторов F1, F2, ..., Fm (обычно m намного меньше n) и характерного фактора иj. Общие факторы описывают корреляции между параметрами, характерный фактор учитывает оставшуюся дисперсию исходных показателей.
Основные этапы современного факторного анализа:
• качественный предварительный анализ экономических явлений и постановка задачи факторного анализа;
• составление массивов исходной информации;
• вычисление и анализ начальной корреляционной матрицы;
• нахождение прямого факторного решения;
• нахождение интерпретируемого факторного решения:
• вычисление факторных коэффициентов;
• содержательная интерпретация факторов;
• анализ и использование полученных результатов. (При помощи такого анализа выявляют и измеряют независимые скрытые факторы для построения аналитической модели.);
• выявление наиболее информативных показателей деятельности;
• соединение информации о независимых аспектах явления в один обобщающий показатель;
• классификация и ранжирование объектов по обобщающим факторам;
• комплексная оценка хозяйственной деятельности.
11.6. Методы комплексной оценки хозяйственной деятельности
В системе управления производством важное значение имеет объективная оценка достигнутого уровня хозяйственной деятельности. Трудность получения такой оценки связана с тем, что хозяйственная деятельность и ее результаты охватывают множество различных процессов и не выражаются одним обобщающим показателем. Поэтому приходится измерять и оценивать различные стороны хозяйственной деятельности и затем объединять частные оценки в единую, комплексную.
В литературе высказывается мнение, что обобщающая (комплексная) оценка экономического процесса или всей хозяйственной деятельности может не иметь законченного экономического содержания, быть «иррациональной» и выведенной искусственно как математическое обобщение частных показателей. Несмотря на это, такая оценка - важный инструмент экономической диагностики хозяйственных систем.
Комплексная оценка должна выражать сущность производственных отношений предприятия: охватывать все главные стороны его производственно-хозяйственной деятельности; включать ограниченное число обобщающих показателей, которое легко поддается обозрению субъектами оценки; быть эластичной (косвенно улавливать динамику общественно необходимых затрат труда), цельной и непротиворечивой. Ее компоненты не должны дублироваться и перемножаться; они должны быть сопоставимы (соизмеримы) с аналогичными показателями у всех объектов, а также один с другим.
Среди методов обобщающей (комплексной) оценки можно выделить описательные и расчетные.
Описательные методы оценки используются для качественной характеристики результатов хозяйственной деятельности, трудно измеримых количественно. Основные недостатки описательных методов оценки: неоднозначность выводов, расплывчатость формулировок, несопоставимость при сравнениях. Тем не менее описательные методы очень важны для стратегических ориентации и широко используются в практике хозяйствования.
Расчетные методы оценки опираются на измеримые показатели деятельности. В основу расчетных методов оценки может быть положен принцип сравнения достигнутого уровня деятельности данной производственной системы с плановым, предшествующим периодом, выявленными общими тенденциями, уровнем других аналогичных систем.
Итак, будем считать, что исходные показатели деятельности вычислены (с необходимой корректировкой) и сведены в таблицу, которую нам удобно,трактовать как матрицу А, состоящую из m строк и п столбцов (где m - число оцениваемых предприятий, л - число исходных показателей).
где аij - j-й показатель i-го предприятия.
Будем считать, что все относительные показатели обладают одинаковой направленностью, причем такой, что большие значения показателей аij соответствуют и лучшим результатам деятельности предприятия.
Теперь перед нами будет стоять задача вычисления некоторого обобщенного комплексного показателя Пj, позволяющего определить место каждого предприятия среди других оцениваемых предприятий.
МЕТОД СУММ. Значение показателя комплексной оценки для каждого предприятия (Пi) рассчитывается как взвешенная сумма результатов его деятельности по сравниваемым показателям, т.е.
Пi = Pj aij , j=1.2,3,...n,
где Рj - весовой коэффициент для j-го исходного показателя.
Чем выше результаты работы предприятия, тем больше значение показателя комплексной оценки.
В современной литературе часто используется понятие предприятия-эталона, с которым сопоставляются все объекты анализа. Некоторые авторы предлагают использовать в качестве такого эталона абстрактное предприятие, у которого все показатели имеют наилучшее значение среди данной совокупности. Практически такой условный эталон строится на основе матрицы А как строка, элементы которой определяются по формуле
a0j = max (aij), i = 1,2,3,…,m, j = 1,2,3,…,n.
Если мы проранжируем каждый столбец матрицы А на ее максимальный .элемент, т.е. на показатель предприятия-эталона, и используем полученную нормативную матрицу А' в качестве исходной для расчета, то получим комплексные показатели
Пi = Pj a'ij , где a'ij = a'ij/ a0j
которые, разумеется, не могут быть больше, чем показатели эталона. Хотя коэффициенты П'j будут близки к определенным выше коэффициентам Пj, распределение мест среди предприятий может несколько измениться, особенно это относится к предприятиям с близкими значениями комплексных показателей.
Основной недостаток метода сумм - уравнивание частных оценок, что требует введения дополнительных весовых коэффициентов при них, определение числовых значений которых представляет самостоятельную сложную проблему.
МЕТОД БАЛЛЬНОЙ ОЦЕНКИ. Разнообразным требованиям удовлетворяет построение комплексной оценки на основе балльных оценок. Баллы, приписываемые исходным показателям, могут быть получены разными способами: либо на основе предварительных соглашений, либо на основе ранжирования значений показателей хозяйственной деятельности. Далее к таблице баллов применяется уже известный метод сумм. Балльный метод позволяет в значительной степени преодолеть трудности оценки, связанные с неоднородностью сравниваемых показателей.
При помощи ранжирования значений исходных показателей осуществляется нормирование разноплановых направлений деятельности в совокупности сравниваемых показателей.
Приведем алгоритм данного метода.
1. Каждый столбец исходной матрицы А изменяется на столбец из номеров мест соответствующих исходных элементов при их ранжировании по убыванию: максимальный элемент заменяется на 1, следующий за ним - на 2 и т.д. Одинаковым по величине исходным элементам присваивается один номер, например п, a следующему за ними элементу - номер (п +1). Таким образом, вместо исходной матрицы А мы получаем новую матрицу В, состоящую из указанных номеров (баллов) bij.
 где bij - место i-го предприятия по j-му показателю.
2. Для каждого предприятия рассчитывается значение показателя комплексной оценки по формуле
Пi = Pj bij , i=1.2,3,...n,
где Pj ? 1 - весовой коэффициент j-го исходного показателя.
Располагая значение показателя Пi в порядке возрастания, можно определить место предприятия среди других в данной совокупности. Первое место занимает предприятие, у которого значение показателя Пi минимальное.
К недостаткам этого простого и наглядного метода относится то, что учитываются только места (баллы) по каждому j-му показателю, величина отставания от предыдущего места (или от первого места) может существенно различаться и искажать оценку.
МЕТОД РАССТОЯНИЙ. В этом методе каждое предприятие рассматривается как точка в п-мерном пространстве: координаты точки - величины исходных относительных показателей, по которым осуществляется сравнение. Тогда расстояние от точки, обозначающей данное предприятие, до точки-эталона будет характеризовать место предприятия в данной совокупности и может приниматься за величину показателя комплексной оценки.
Если в качестве предприятия-эталона выбрано такое, у которого все показатели имеют наилучшие значения среди данной совокупности, то для расчета показателей комплексной оценки необходимо использовать нормированную матрицу A':
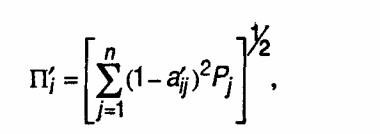 где a'ij (j = 1,2,3,..., n) - элементы матрицы А', определяемые через элементы aij исходной матрицы A как a'ij = a'ij /а0j;
Рj ? 1 - весовой коэффициент для j-го исходного данного:
а0j = max (aij ).
Таким образом, метод расстояний обладает рядом неоспоримых преимуществ. Метод достаточно наглядный и позволяет осуществить достаточно гибкий подход к оценке деятельности разных предприятий. Кроме того, согласно данному методу исходные данные рассматриваются как независимые, перекрывающиеся, недублирующиеся и отождествляются с независимыми координатами п-мерного пространства.
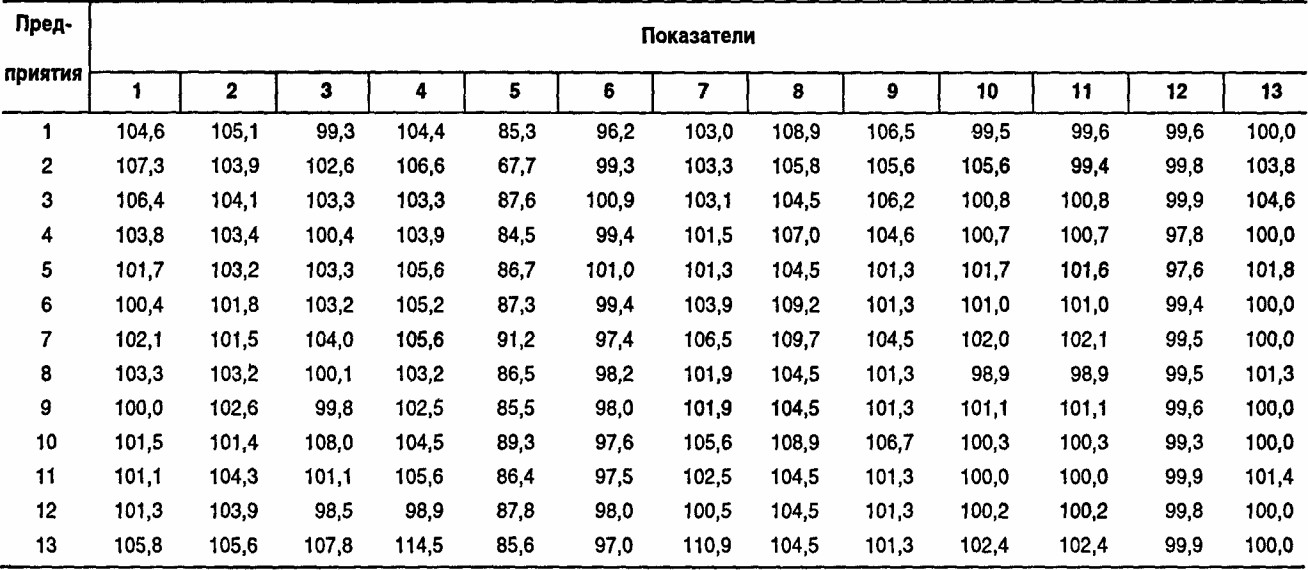
РАСЧЕТ ПОКАЗАТЕЛЕЙ КОМПЛЕКСНОЙ ОЦЕНКИ ПРИ ПОМОЩИ БАЛЛЬНОГО МЕТОДА, МЕТОДА СУММ И МЕТОДА РАССТОЯНИЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЙ. Мы рассмотрим такой расчет на примере 13 предприятий одного из АО. В последних двух методах расчет выполняется дважды: сначала для исходной матрицы А, а затем для нормированной матрицы А'. Как обсуждалось выше, в первом случае это соответствует сопоставлению с эталоном, имеющим по всем показателем уровень выполнения плана 100%, во втором случае сопоставление проводится с условным предприятием, у которого все показатели имеют наилучшие значения среди данной совокупности предприятий.
Пример. Исходные данные приведены в таблице на с. 293, а результаты расчетов - в таблице на с. 294. Метод сумм и метод расстояний дают очень близкие между собой распределения мест предприятий АО, а балльный метод - несколько отличающееся от них распределение мест. Распределение мест, полученное по методу расстояний, отличается от распределения мест, полученного по методу сумм, лишь тем, что место 1-го предприятия изменяется с 8-го (по методу расстояний) на 7-е (по методу сумм); место 4-го предприятия изменяется соответственно с 10-го на 9-е; место 5-го предприятия- с 7-го на 8-е; место 11-го предприятия - с 9-го на 10-е; места остальных предприятий совпадают. Сравнивая балльный метод, например, с методом сумм, мы находим только 4 предприятия (из 13), имеющих одинаковые места; места остальных 9 предприятий различаются, вплоть до разницы в 3 места (5-е предприятие). Нормирование исходной матрицы, т.е. переход
Выполнение плана по основным показателям деятельности предприятий АО
(%)
 Показатели комплексной оценки при расчете по различным методам для предприятий АО
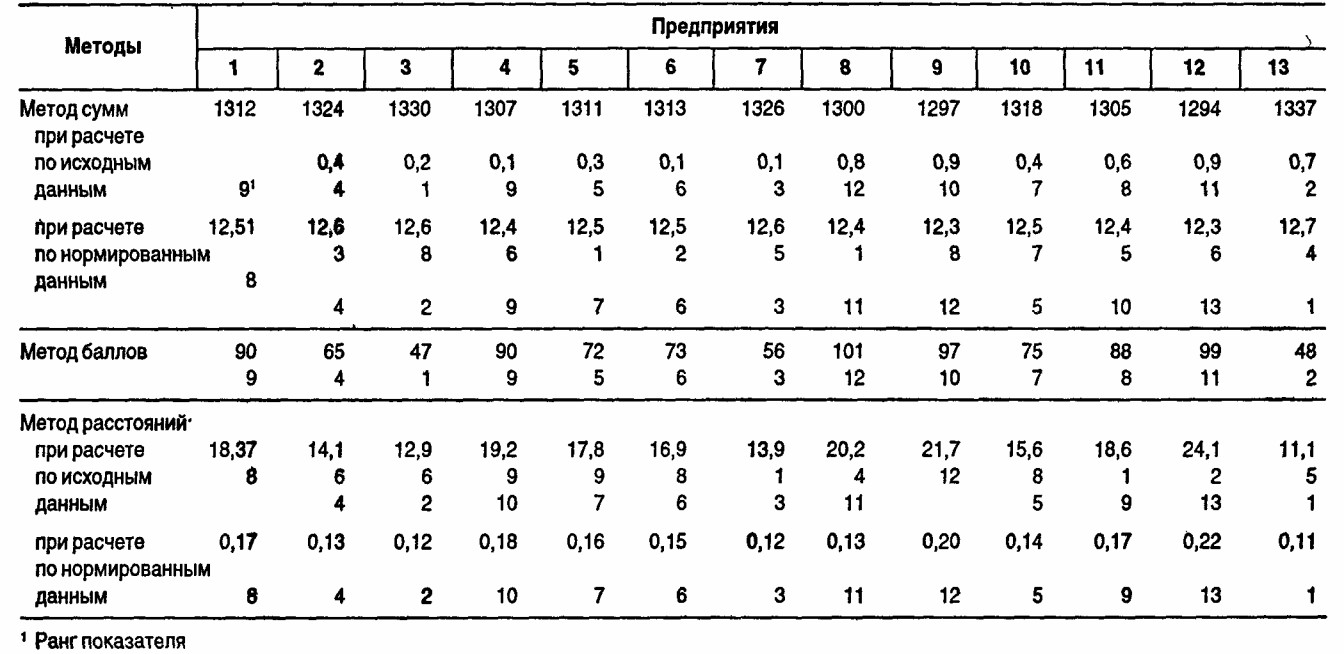 от одного предприятия-эталона к другому, в методе расстояний не изменило распределение мест среди предприятий, а в методе сумм привело к тому, что 1-е и 5-е предприятия поменялись местами: 1-е предприятие перешло с 7-го на 8-е место, а 5-е предприятие, наоборот, с 8-го на 7-е место.
Резюме
Количественные методы анализа, рассмотренные в данной главе, являются важным подспорьем в принятии управленческих решений. В последующих главах читатель встретится также с многими примерами их применения.
Материал раздела 11.1 дает представление о полном арсенале количественных методов в упорядоченном виде.
Разделы 11.2 и 11.4 помогают уяснить принципиальные различия между детерминированным (функциональным) и стохастическим (вероятностным) подходами к исследованию факторных систем хозяйственной деятельности.
Разделы 11.3, 11.5, 11.6 дают инструментарий количественной оценки факторных влияний на результаты хозяйственной деятельности как в единичных случаях (расчет влияния изменения численности персонала на объем производства и др.), так и в массовых процессах, выраженных пространственной или временной (динамической) выборкой анализируемых показателей.
Приложение 1. Домашние упражнения
Задание 1. Применение методов факторного анализа
Задачи пунктов 1-6 решаются как методом цепных подстановок, так и интегральным методом. Для решения задачи п. 6 интегральным методом необходимо воспользоваться различными формулами или непосредственно вывести их из общих формул, предположив, что факторы изменяются линейно.
1. Проанализируйте влияние использования производственных фондов на объем продукции по приведенным данным:
4. Проанализируйте влияние изменений численности производственного персонала и средней заработной платы на отклонение фактического фонда заработной платы от планового по приведенным данным:
 Результаты расчетов представьте в виде таблицы;
 5. Проанализируйте влияние средней стоимости остатков нормируемых оборотных средств и выручки от реализации продукции на количество оборотов (прямой коэффициент оборачиваемости) оборотных средств по приведенным данным:
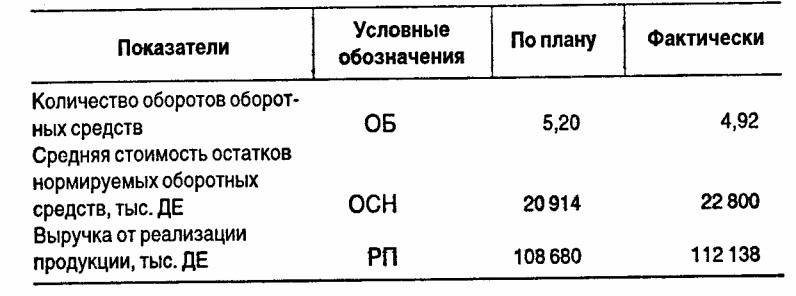 Результаты расчетов представьте в виде таблицы:
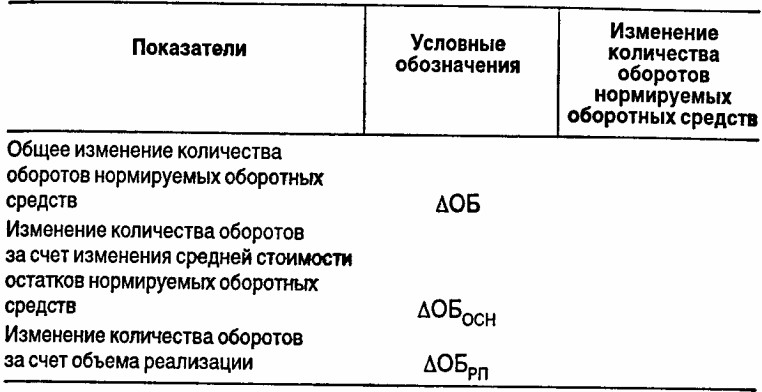 6. Проанализируйте влияние прибыли на 1 ДЕ реализованной продукции, фондоотдачи и количества оборотов нормируемых оборотных средств на изменение коэффициента общей рентабельности по приведенным данным:
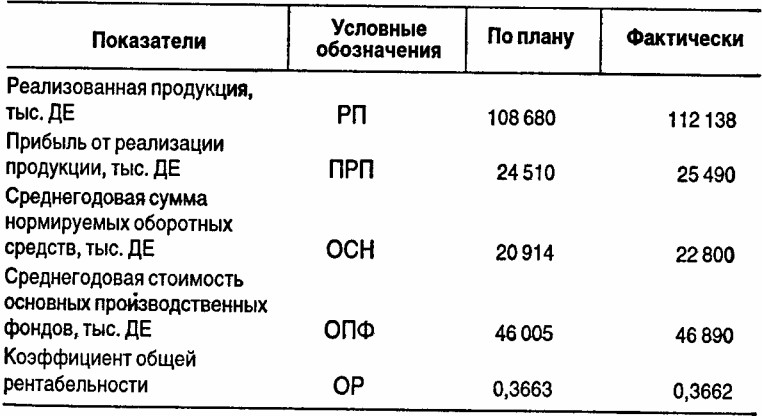 Указание. Необходимо преобразовать формулу расчета коэффициента общей рентабельности таким образом:
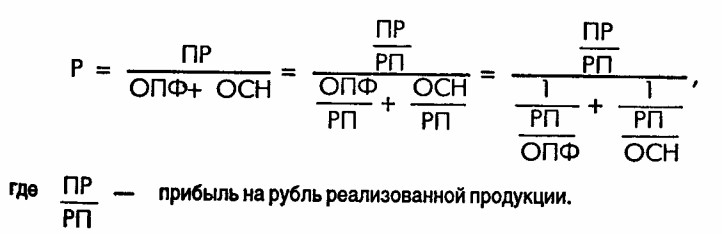 Таким образом, исходной для расчета является формула
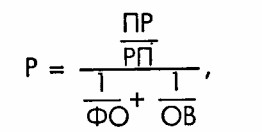 где ФО - фондоотдача основных производственных фондов;
OB - количество оборотов нормируемых обор.отных средств.
Результаты расчетов представьте в виде таблицы:
 Задание 2. Анализ регрессий
1. Дайте оценку тренда по данным о выпуске автомобилей (табл. 1). Рассчитайте статистические оценки параметров регрессионного уравнения.
2. Проанализируйте по данным табл. 2 тренды выпуска продукции (валовой, товарной). Проведите сравнительный анализ полученных уравнений.
 3. Рассчитайте параметры регрессионного уравнения по данным табл. 3, где зависимой переменной является фондоотдача, а независимой - соотношение активной и пассивной частей основных производственных фондов. Дайте оценку качества полученного уравнения.
 Задание 3. Применение методов комплексной оценки
1. По данным табл. 4:
а) проведите комплексную оценку работы подразделений методом суммы мест;
б) проведите комплексную оценку работы подразделений методом суммы баллов, установив для показателей в качестве оценочной шкалы отрезок [0,5];
в) проведите комплексную оценку работы подразделений методом расстояний;
г) сопоставьте результаты расчетов по всем методам, сделав сводную таблицу результатов.
2. Проведите оценку значимости показателей, присвоив каждому показателю соответствующий уровень значимости, стимулирующий подразделения к развитию интенсивных форм хозяйствования.
Таблица 4 _____(%)
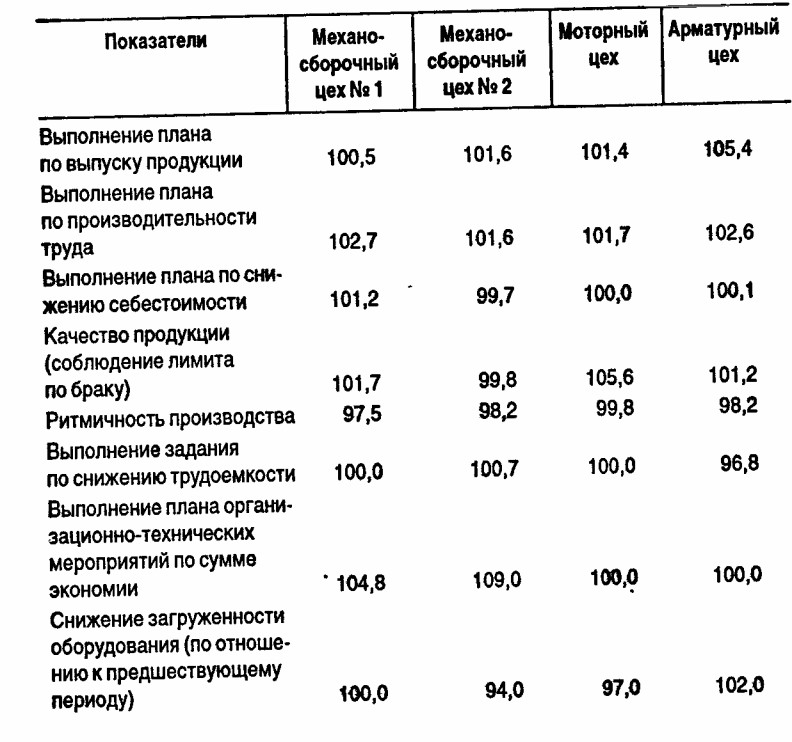 Продолжение
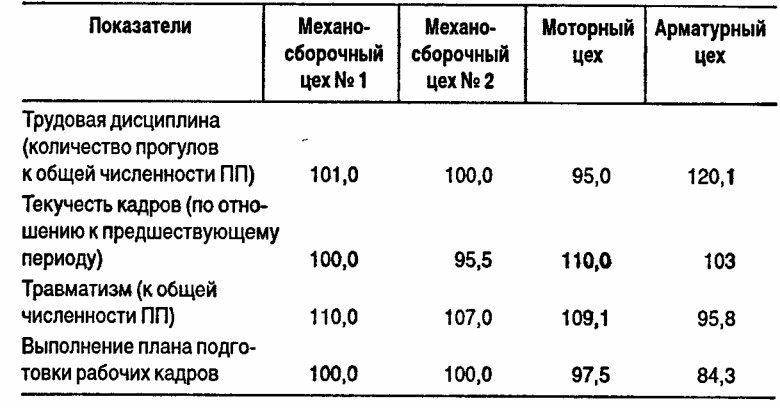 3. Проведите комплексную оценку работы подразделений методом суммы мест. Результаты решения сравните с результатами п. 3. Выявите и объясните причины различий.
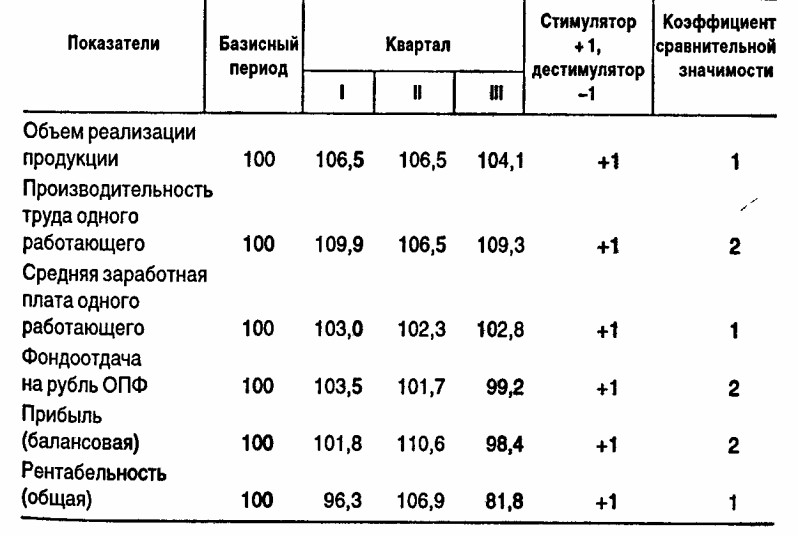
4. По данным табл. 5 проведите комплексную оценку динамики развития цеха: методом суммы мест; методом балльной оценки; методом расстояний. Сопоставьте результаты.
Таблица 5 (в % к предыдущему периоду)
 Приложение 2. Вопросы для самопроверки
1. Что дает применение математических методов и ПЭВМ в анализе хозяйственной деятельности?
2. Охарактеризуйте основные методы анализа.
3. В чем суть метода удлинения факторной системы? расширения? сокращения?
4. Определите влияние факторов методом цепных подстановок для зависимостей вида: z = х + у; z = х • у; z = х/у.
5. Каковы достоинства интегрального метода факторного анализа?
6. Назовите необходимые условия применения корреляционно-регрессионного анализа.
7. Что показывают коэффициенты регрессии?
8. Перечислите методы комплексной оценки хозяйственной деятельности и дайте им краткую характеристику.
9. Укажите достоинства и недостатки различных методов комплексной оценки.
|
© 2006 "Управленческий учет Под редакцией А.Д. Шеремета". Все права защищены, по всем вопросам
|